Embark on a captivating journey with the Unit 1 AP Stats Practice Test, your ultimate guide to mastering the fundamentals of statistical analysis. Dive into a world of data, probability, and hypothesis testing, and emerge as a statistical virtuoso.

This comprehensive practice test will equip you with the knowledge and strategies to tackle any AP Statistics exam with confidence. Prepare to uncover the secrets of data analysis, probability distributions, and hypothesis testing, and unlock your potential as a statistical thinker.

Practice Test Overview

The Unit 1 AP Stats practice test is an essential tool for students preparing for the actual exam. It helps familiarize students with the structure, question types, and content of the exam. By taking this practice test, students can identify areas where they need improvement and focus their studies accordingly.

Types of Questions and Topics Covered

The practice test covers a wide range of topics from Unit 1, including:

• Exploring Data
• Sampling and Experimentation
• Probability
• Random Variables

The test includes various question types, such as multiple-choice, free-response, and problem-solving questions. These questions assess students’ understanding of concepts, their ability to apply statistical methods, and their problem-solving skills.

General Strategy for Approaching the Test

To approach the practice test effectively, students should:

• Review the course material thoroughly.
• Time themselves while taking the test to simulate the actual exam conditions.
• Attempt all questions, even if they are unsure of the answer.
• Read the questions carefully and identify the key information.
• Show all their work for partial credit.

By following these strategies, students can maximize their performance on the practice test and improve their preparation for the actual AP Stats exam.

Data Analysis and Statistical Methods

Data analysis is the process of extracting meaningful information from data. Statistical methods are used to analyze data and draw conclusions from it.

Descriptive statistics are used to summarize data. The mean, median, mode, range, and standard deviation are all descriptive statistics. The mean is the average of a set of data. The median is the middle value of a set of data.

The mode is the value that occurs most often in a set of data. The range is the difference between the largest and smallest values in a set of data. The standard deviation is a measure of how spread out a set of data is.

Histograms, box plots, and scatterplots are all graphical representations of data. Histograms show the distribution of data. Box plots show the median, quartiles, and outliers of a set of data. Scatterplots show the relationship between two variables.

Sampling distributions are the distributions of sample statistics. The Central Limit Theorem states that the sampling distribution of the mean is approximately normal, regardless of the shape of the population distribution.

Descriptive Statistics

Descriptive statistics are used to summarize data. The mean, median, mode, range, and standard deviation are all descriptive statistics.

• The mean is the average of a set of data.
• The median is the middle value of a set of data.
• The mode is the value that occurs most often in a set of data.
• The range is the difference between the largest and smallest values in a set of data.
• The standard deviation is a measure of how spread out a set of data is.

Graphical Representations of Data

Histograms, box plots, and scatterplots are all graphical representations of data.

• Histograms show the distribution of data.
• Box plots show the median, quartiles, and outliers of a set of data.
• Scatterplots show the relationship between two variables.

Sampling Distributions and the Central Limit Theorem

Sampling distributions are the distributions of sample statistics. The Central Limit Theorem states that the sampling distribution of the mean is approximately normal, regardless of the shape of the population distribution.

• The sampling distribution of the mean is approximately normal.
• The mean of the sampling distribution of the mean is equal to the population mean.
• The standard deviation of the sampling distribution of the mean is equal to the population standard deviation divided by the square root of the sample size.

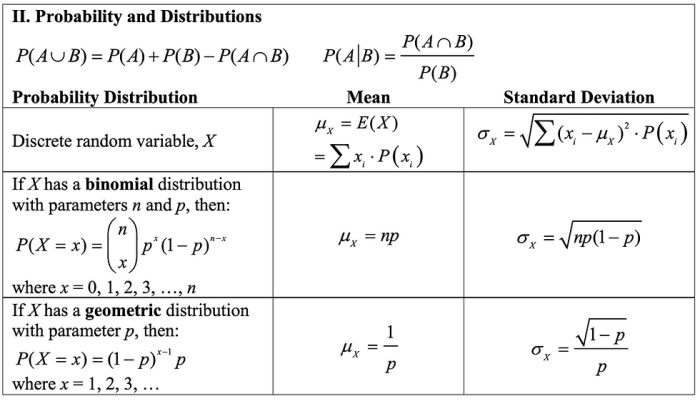
Probability and Distributions

Probability is a branch of mathematics that deals with the likelihood of events occurring. It provides a framework for quantifying uncertainty and making predictions based on available information.

Probability distributions are mathematical functions that describe the probability of different outcomes in a random experiment. They are essential for understanding the behavior of random variables and making inferences about populations from sample data.

Conditional Probability

Conditional probability measures the probability of an event occurring given that another event has already occurred. It is denoted as P(A|B), where A is the event of interest and B is the condition.

Independence, Unit 1 ap stats practice test

Two events are independent if the occurrence of one event does not affect the probability of the other event occurring. In other words, P(A|B) = P(A).

Discrete Probability Distributions

Discrete probability distributions describe the probability of obtaining specific, countable values. Some common discrete distributions include:

• Binomial distribution: Models the number of successes in a sequence of independent experiments.
• Poisson distribution: Models the number of events occurring within a fixed interval of time or space.

Continuous Probability Distributions

Continuous probability distributions describe the probability of obtaining values within a continuous range. Some common continuous distributions include:

• Normal distribution: Models the distribution of many real-world phenomena, such as heights and weights.
• t-distribution: Similar to the normal distribution, but used when the sample size is small.

Sampling Distributions

Sampling distributions describe the distribution of sample statistics, such as means or proportions, calculated from repeated random samples from a population.

If you’re looking for some extra practice for your Unit 1 AP Stats test, check out the BJU World Studies 4th Edition . This book is packed with practice problems and helpful explanations that will help you prepare for the exam.

Don’t forget to also review your notes and practice taking practice tests to ensure you’re fully prepared for the Unit 1 AP Stats test.

Central Limit Theorem

The Central Limit Theorem states that the sampling distribution of means approaches the normal distribution as the sample size increases, regardless of the shape of the population distribution.

Confidence Intervals and Hypothesis Testing

Confidence intervals and hypothesis testing are fundamental statistical tools that allow us to make inferences about a population based on sample data. These techniques are widely used in various fields to draw conclusions and make informed decisions.

In this section, we will explore the concepts of confidence intervals and hypothesis testing, their applications, and the steps involved in conducting them.

Confidence Intervals

A confidence interval is a range of values that is likely to contain the true population parameter with a certain level of confidence. It is constructed based on sample data and a chosen confidence level.

• Formula:$CI = \barx \pm z^* \fracs\sqrtn$ where – $\barx$ is the sample mean – $z^*$ is the critical value from the standard normal distribution corresponding to the desired confidence level – $s$ is the sample standard deviation – $n$ is the sample size
• Interpretation:With a certain level of confidence, we can say that the true population mean lies within the calculated confidence interval.
• Applications:Confidence intervals are used to estimate population parameters, such as the mean or proportion, and to assess the precision of the estimates.

Hypothesis Testing

Hypothesis testing is a statistical procedure used to determine whether there is sufficient evidence to reject a null hypothesis in favor of an alternative hypothesis. It involves comparing the observed sample data to the expected results under the null hypothesis.

• Steps:
  1. State the null and alternative hypotheses:The null hypothesis ($H_0$) represents the claim being tested, while the alternative hypothesis ($H_1$) is the opposite claim.
  2. Set the significance level:This is the maximum probability of rejecting $H_0$ when it is actually true (Type I error).
  3. Calculate the test statistic:This is a measure of how far the sample data deviate from the expected results under $H_0$.
  4. Determine the p-value:This is the probability of obtaining a test statistic as extreme as or more extreme than the observed value, assuming $H_0$ is true.
  5. Make a decision:If the p-value is less than the significance level, we reject $H_0$ in favor of $H_1$. Otherwise, we fail to reject $H_0$.
• Types of hypothesis tests:
  • One-sample tests:Compare the sample data to a known population value.
  • Two-sample tests:Compare the sample data from two different populations.
• Applications:Hypothesis testing is used in various fields to test claims, make inferences, and draw conclusions based on data.

Applications and Real-World Examples

AP Statistics concepts find practical applications in numerous fields, ranging from scientific research to business and finance. Statistical methods empower us to analyze data, draw meaningful conclusions, and make informed decisions.

It’s crucial to consider the ethical considerations and limitations of statistical methods. Responsible use of statistics ensures that results are accurate, unbiased, and not misinterpreted.

In today’s data-driven world, statistical literacy is paramount. It enables individuals to critically evaluate information, make informed choices, and navigate the complexities of a world awash in data.

Real-World Applications

Statistical concepts are indispensable in various fields:

• Medicine:Clinical trials use statistical methods to assess the efficacy and safety of new treatments.
• Business:Market research and customer surveys rely on statistics to understand consumer behavior and improve products.
• Finance:Statistical models are used to predict stock prices, manage risk, and optimize investment strategies.
• Environmental Science:Statistics help researchers analyze environmental data, monitor trends, and predict the impact of human activities on the ecosystem.
• Education:Statistical methods are used to evaluate teaching effectiveness, assess student performance, and identify areas for improvement.

Ethical Considerations and Limitations

While statistical methods are powerful tools, it’s important to be aware of their limitations and ethical implications:

• Sampling Bias:Non-representative samples can lead to biased results.
• Confounding Variables:Uncontrolled variables can distort relationships between variables.
• Misinterpretation:Statistics can be misinterpreted or misused to support false claims.
• Ethical Use:Statistics should not be used to manipulate or deceive.

Importance of Statistical Literacy

In an increasingly data-driven world, statistical literacy is essential:

• Critical Thinking:Statistics helps individuals evaluate information critically and make informed decisions.
• Informed Decision-Making:Statistical knowledge empowers individuals to understand and navigate data-driven arguments.
• Data Interpretation:Statistical literacy enables individuals to interpret data and draw meaningful conclusions.
• Problem-Solving:Statistics provides tools for solving real-world problems involving data.
• Career Opportunities:Statistical skills are in high demand in various industries.

Helpful Answers: Unit 1 Ap Stats Practice Test

What is the purpose of the Unit 1 AP Stats Practice Test?

The practice test is designed to assess your understanding of the foundational concepts of AP Statistics, including data analysis, probability, and hypothesis testing.

What types of questions are included in the practice test?

The practice test covers a wide range of question types, including multiple-choice, free-response, and data analysis questions.

How can I use the practice test to prepare for the AP Statistics exam?

By completing the practice test, you can identify areas where you need additional review, practice applying statistical concepts, and build your confidence for the actual exam.